CPU供应商 ET200MP有源背板模块代理商西门子触摸屏代理商
西门子变频器代理商,荆门西门子PLC模块授权一级代理商,湖北西门子电线电缆授权代理商,上海西门子S7-200CPU系列代理商,西门子S7-1200CPU系列代理商,西门子西门子模块授权一级代理商,西门子西门子低压一级供应商,西门子低压断路器代理商,西门子S7-500系列代理商
| Siemens | CPU模块 | 6ES7416-3FS06-0AB0 |
| Siemens | WINCC软件 | 6AV6381-2BC07-5AV0 |
| Siemens | WINCC软件 | 6AV6381-2BH07-5AV0 |
| Siemens | WINCC软件 | 6AV6381-2BM07-5AV0 |
| Siemens | WINCC软件 | 6AV6381-2BS07-5AV0 |
| 西门子 | 模块 | 6ES7155-6AU01-0CN0 |
| 西门子 | 交换机 | 6GK5204-0BA10-2BA3 |
下图33-1的(1)所示为简单RLC串联交流电路。若给该电路通以直流电,由于电容元件的隔断直流的作用,该电路中是没有电流流过的。但给它通以正弦交流电时,根据我们上次所学的内容,该电路除了会有电阻外,还会有感抗和容抗的存在。这里的电阻、电感和电容之间的关系又是怎样的呢?

图33-1
在同一交流电路中,各电气量的角频率ω(频率f)都是相同的,这在之前我们学习正弦量的时候已经提过。回顾上一次的学习内容,在R、L、C的各个单一参数交流电路中,流过电阻元件的电流与电阻元件两端的电压同相;流过电感元件的电流滞后于电感元件两端的电压90°;流过电容元件的电流超前于电容元件两端的电压90°,感抗XL=ωL,即U =IXL,且容抗XC=1/ωC,即U =IXC,结合已知条件:电流的瞬时值表达式和相量式,我们就可以推理出RLC串联交流电路的电压和电流关系。


如上图33-1的(2)瞬时值表达式和(3)相量式。在图33-1的(2)式中,计算变换过程大家看看即可,由电压u的瞬时值表达式中,我们可以看到,RLC串联交流电路的电压等于各个元件两端电压瞬时值的代数之和,而不是有效值的简单相加,还要考虑相位关系。
同理,图33-1的(3)相量式更为直观,从电压的相量式中,我们可以看到,其虚部(即乘以90°旋转因子部分)是感抗和容抗的差,这是因为感抗和容抗两者上的电压方向一个滞后电流90°,一个超前电流90°,相互抵消。
根据图33-1(3)的电压相量式,即电压相量等于电流相量乘以某定值(频率不变)的这种表达式,定义阻抗Z(又称复阻抗),如下图33-2所示,它是由电路参数决定。
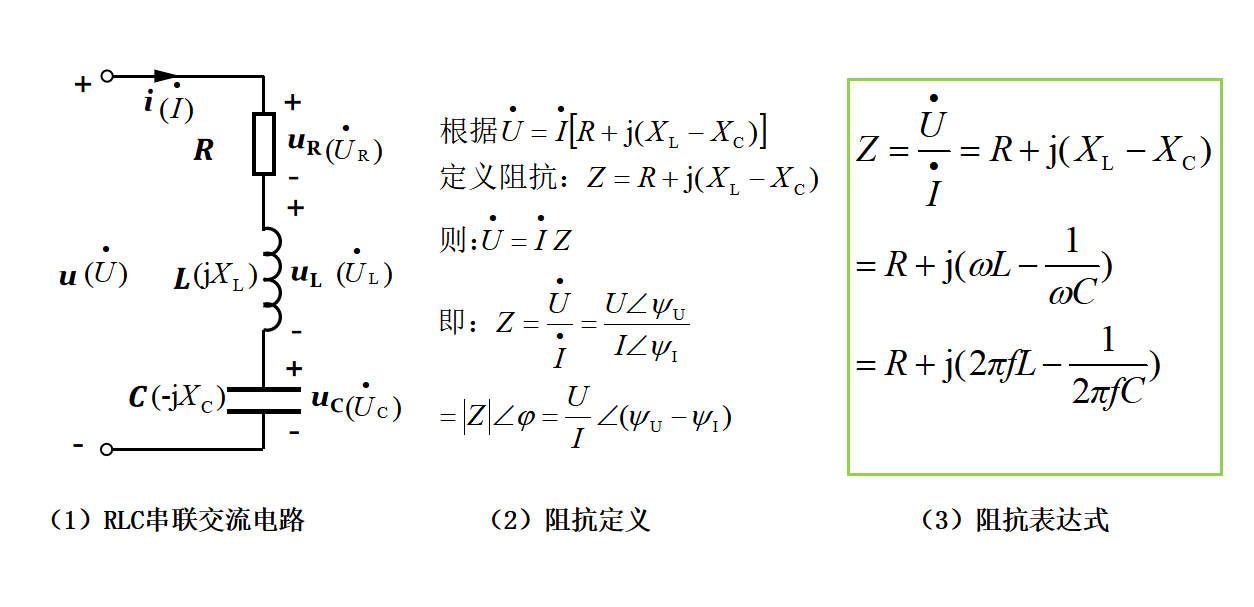
图33-2
图33-2(2)所示的阻抗,定义为电压与电流的比值,常用Z表示,单位是欧姆(Ω)。阻抗也是一个复数,其实部称为电阻R,虚部称为电抗X,这在上一次的学习中也有所提及。这里要提醒的一点是,阻抗不是相量,这是因为相量是正弦量的表示形式,而阻抗不是正弦量,阻抗符号Z上面不能像电压相量、电流相量那样在上面加点。

根据阻抗的定义,从电压相量除以电流相量的值中,可以发现,阻抗的模(大小)为电压有效值U与电流有效值I的比值,而辐角为电压u与电流i的相位差。根据感抗与容抗的定义、角频率与频率的关系,可得阻抗的集中表达式,如图33-2(3)所示,这几种表达式在电路分析中都比较常用,所有大家很有必要熟记。
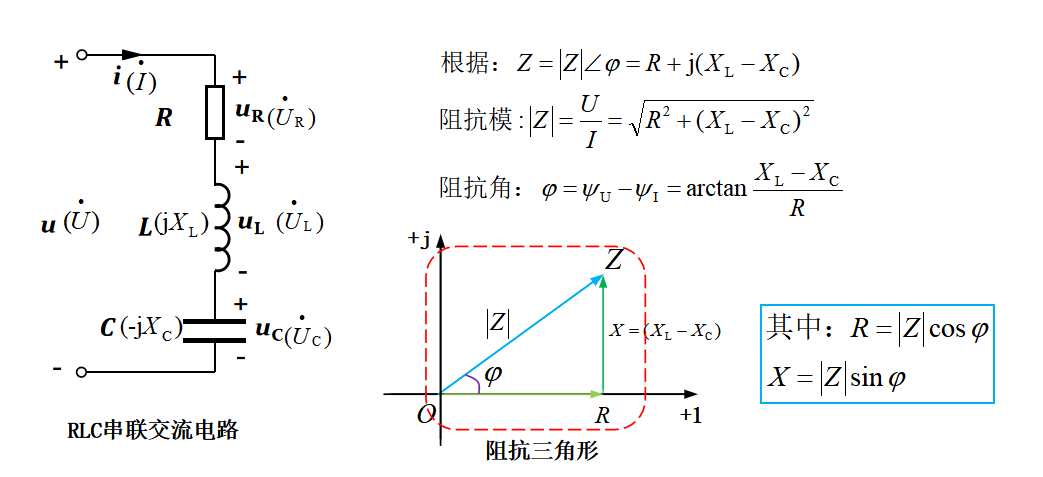
图33-3
阻抗由电阻和感抗、容抗组成,当电路中没有电感元件时,显然,电路中也就不会有感抗,即此时阻抗中只有电阻和容抗;同理,当电路中没有电容元件时,显然,电路中也就不会有容抗,即此时阻抗中只有电阻和感抗。
阻抗既然是一个复数,那么它显然可以在复平面上表示,如图33-3所示。根据阻抗在复平面上的表示,可以看到,其电阻、电抗与阻抗组成一个三角形,这就是大家平常所说的阻抗三角形,图示的阻抗三角形中感抗大于容抗,即X=XL-XC>0,此时的辐角大于零。阻抗模就是上文所说的电压有效值U与电流有效值I的比值,阻抗角为电压u与电流i的相位差。
显然,阻抗、电阻、电抗和阻抗角之间可以用三角函数进行转化和计算,例如阻抗角可以用电阻和电抗的反正切函数关系求得,已知阻抗值的情况下用余弦函数和正弦函数求得电阻和电抗,如图33-3所示。
电抗为感抗与容抗的差,即X=XL-XC,结合阻抗三角形,可以得到以下电路参数与电路性质的关系如图33-4所示。
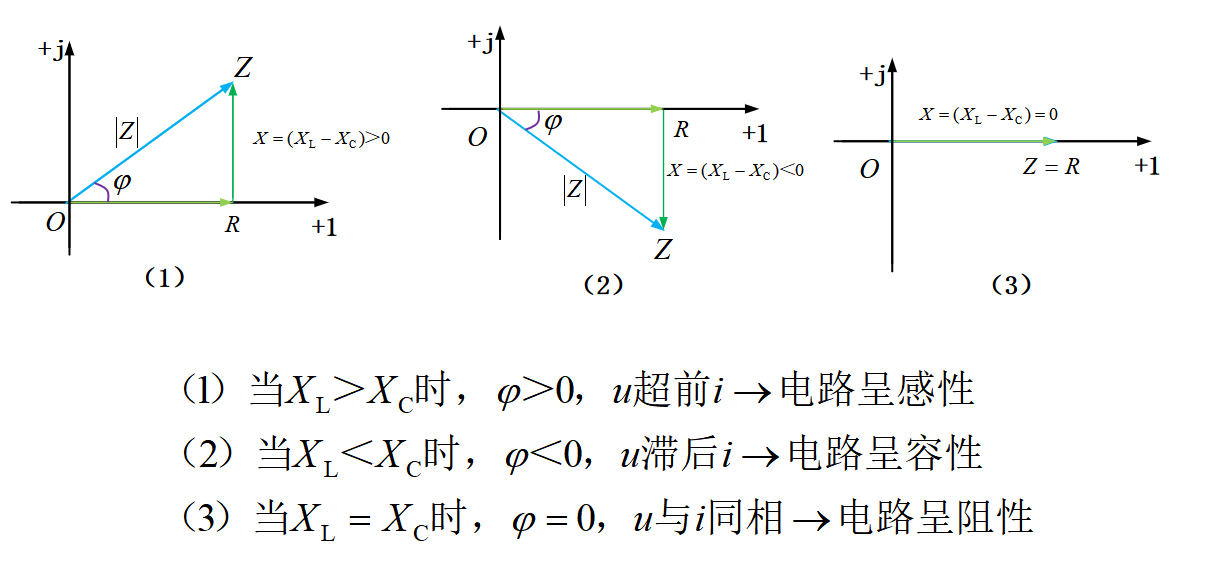
图33-4
根据图33-4中内容,当感抗与容抗的差不电路会呈现不同的性质,相角也会随之变化。当感抗大于容抗时,电路呈感性,此时阻抗角大于零,即电路中电压超前电流;当容抗大于感抗时,电路呈容性,此时阻抗角小于零,即电路中电压滞后电流;而当感抗等于容抗时,两者大小相等方向电抗为零,此时电路呈阻性,电压与电流同相。
实际工作中的电容补偿,其依据其实就是电路中感抗和容抗的不同关系,例如在感性负载(如交流电动机)的交流电路中,此时电压超前电流,为了减小电压与电流之间的相角(即功率因数角),可以在电路中适当接入电容器,以抵消电路中的部分感抗,使得阻抗角变小,提高有功功率。
当补偿后电路依然呈感性,这种补偿方式称为欠补偿;当完全补偿时,即补偿后电路依然呈阻性,这种补偿方式称为全补偿;当补偿后电路依然呈容性,这种补偿方式称为过补偿。

在RLC串联交流电路中,当以电流相量为参考相量时,各元件的电压是由该元件的参数(电阻、电感、电容)所决定的,包括其数值和相角。结合阻抗三角形和电压电流关系,可以画出电压三角形如下图33-5所示。
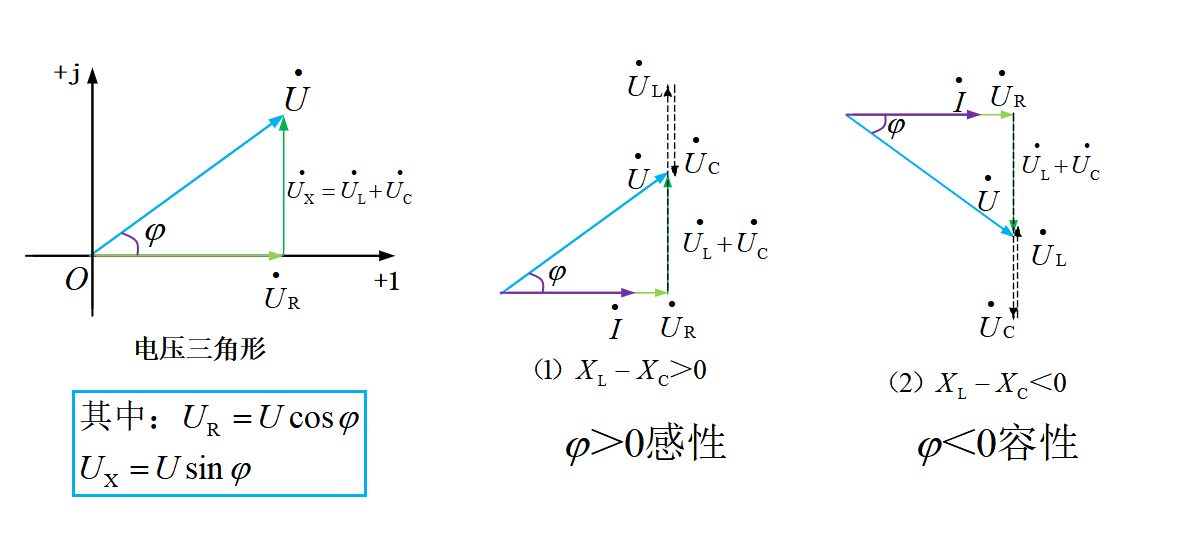
图33-5
根据图33-5所示可以发现,电压三角形的相角其实和阻抗角相等,这是因为在交流电路中,根据图33-2中阻抗的定义,电流相角已知的情况下,电压相角就是由电路参数(即电阻、电感和电容)所决定。
结合我们之前所学的相量运算,当感抗大于容抗时,如图33-5(2)所示,电阻电压相量、电感电压相量与电容电压相量相加,各元件电压相量首尾相连,此时电压与电流的相角大于零,电路呈感性,同理可以得到电路呈容性时的电压三角形如图33-5(3)所示。
在上一次学习了单一参数交流电路时,我们知道了电阻元件在交流电路中总是消耗电能的,而电感元件和电容元件是储能元件,它们不消耗电能,只是和电源进行能量的交换。举一反三,在RLC串联交流电路中,因为存在电阻、电感和电容,电路在是在消耗电能的还进行着能量的交换。此时,该RLC串联交流电路的功率关系如下图33-6所示。

图33-6
图33-6的各个功率计算过程大家可以不管,只需记得终结果即可。在图33-6(1)所示的瞬时功率表达式中,其两个相加项有着不同的含义,左边部分的值总是大于零,代表了耗能元件上的瞬时功率;
而右边部分有大于零和小于零两种情况,代表了储能元件上的瞬时功率。也就是说,在每一瞬间,电源提供的功率一部分被耗能元件消耗掉,一部分与储能元件进行能量交换。

根据图33-6(2)所示的平均功率表达式,平均功率(又称有功功率)P为电压与电流乘积的余弦值,其中cosφ称为功率因数,它是用来衡量负载对电源的利用程度。结合上次所学的无功功率知识,得RLC串联交流电路无功功率为图33-6(3)所示,其中(XL-XC)表明电感和电容与电源之间的能量互换。

图33-7
根据电压三角形,把电阻电压有效值乘以电流有效值即为有功功率的值,它是总电压与总电流有效值乘积的余弦值;
同理,把电抗电压有效值乘以电流有效值即为无功功率的值,它是总电压与总电流有效值乘积的正弦值。根据有功功率和无功功率的这种三角函数关系,定义视在功率S如下图33-8所示,它是电路中总电压与总电流有效值的乘积,用符号S表示,单位是伏安(VA)。

图33-8
和阻抗三角形一样,有功功率、无功功率与视在功率在复平面上也可以组成功率三角形。显然,视在功率也不能用相量表示,因为它不是正弦量。比较阻抗三角形、电压三角形和功率三角形,可以发现,它们之间是由关联的,即将电压三角形的有效值同除电流有效值,就可以得到阻抗三角形;将电压三角形的有效值同乘电流有效值,就可以得到功率三角形。

在电路中,电阻、电感和电容都可以进行串并联,而由电阻、电感和电容组成的阻抗显然也可以进行串并联。我们这次就先学习阻抗的串联,下次再学习阻抗的并联。
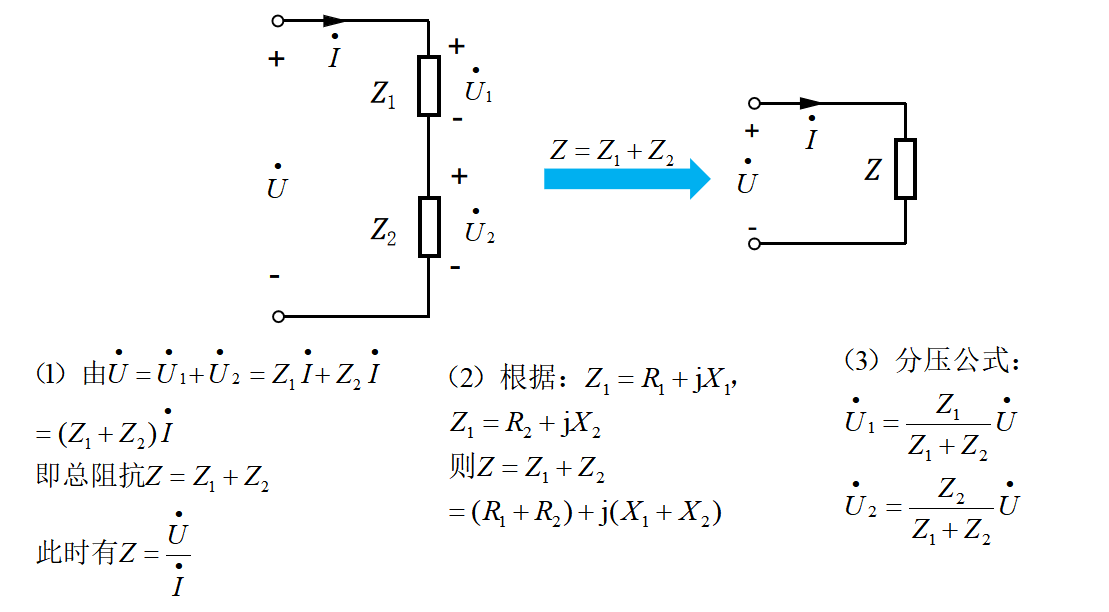
图33-9
电阻的串联是将各电阻直接相加得到等效总电阻,流过各个电阻的电流一样,各个电阻上的电压之和为总电压......阻抗的串联其实和电阻的串联很相似,也是将各个串联阻抗相加得到等效总阻抗,如图33-9(1)所示。
不同的是,阻抗的相加并不是简单的数值相加,而是复数的运算,如图33-9(2)所示,;两个阻抗相加,分别将其实部与实部相加得到电阻部分的值,虚部与虚部相加得到电抗部分的值。
阻抗串联交流电路中,各个阻抗对总电压也有分压作用,此时的分压是相量的运算,如图33-9(3)所示。
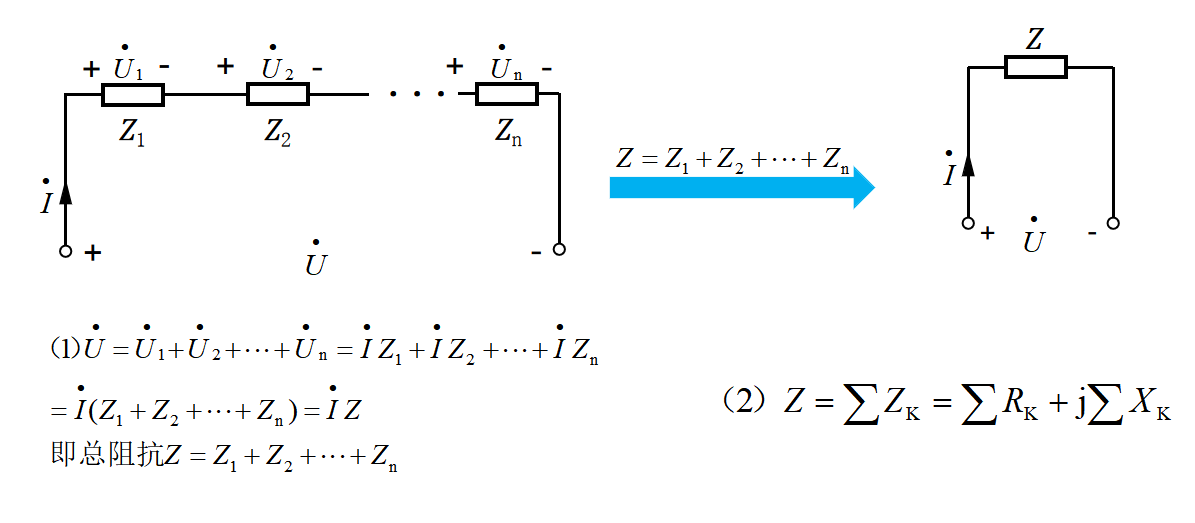
图33-10
将图33-9(1)式进行推广,得到多阻抗串联电路的一般式,如上图33-10所示。显然,多阻抗串联电路的等效变换理解起来并不难,其实际的计算相对麻烦,因为其中涉及到数值与角度相互关联。


CPU供应商 ET200MP有源背板模块代理商西门子触摸屏代理商西门子电源模块代理商西门子PLC模块代理商西门子CPU模块代理商西门子电源模块代理商西门子交换机代理商西门子电机代理商