海口西门子专业授权代理商

各种电机(包括直线电机)，从磁场观点去看，其运动均可视为定子磁场与转子磁场相互作用之结果，而且两磁场间保持相对静止，只是其作用角(两磁场间夹角)不同而已。

直流电机：定子磁场为一固定磁场，转子磁场与定子磁场相互垂直，并保持空间相对位置不变。

异步电机：定子磁场为旋转磁场，转子中导体切割定子旋转磁场，产生感应电流，并在转子中形成感应磁场，该磁场跟随定子磁场同步运行，两磁场间夹角近似为90o。

同步电机：定子磁场为旋转磁场，转子电枢被直流激励为一固定磁场，定子磁场与转子磁场同步旋转两磁场夹角为0o。

步进，无论是反应式或混合式，都不外乎是一个转子无外加励磁电流的同步电机。在定子磁场激励后，转子磁场与定子磁场同步运行，并在空间的位置保持相对静止，即夹角为0o，也就是处于*小磁阻状态。当转子与定子的“同步角差”大于步距角的一半时’则发生“失步”现象。

步进电动机的定子磁场激励方法，除了因电机绕组相数不同而异外，即使是同一电机，也有不同方式，于是便产生了许多驱动电路。但归结起来，这些旨在使步进电动机按“步进”方式运行的常规线路，在步进电动机定子中所激励的磁场都是“步进”的脉动旋转磁场。它们在不同程度上使用步进电动机的运转特性存在着低速振荡、高速力矩小，共振、失步、分辨率低、功耗大等缺点，以致不能达到和满足对步进电动机执行伺服所提出的高精度和高速度的要求。

对步进电动机的这些缺点，提出了新的驱动概念一步进电动机同步矢量运转方式，并研制成功了sv系列步进电动机同步矢量伺服系统。

1系统计算机理论依据

基于步进电动机在磁场作用原理上的上述特点，设想在步进电动机定子中产生一个具有恒模场强的均匀连续旋转磁场，使步进电动机在该场的作用下同步平滑地运转。现以三相步进电动机为例，简述其原理。

在步进电动机定子中要形成的均匀圆周旋转磁场，如图1所示。设p点为单位圆上的任意一点，矢量筇沿圆周均匀旋转，模lopl等于常数；为此，要建立一个数学模型，使三相绕组中流过的励磁电流，在任意转角都产生一满足上述要求的合成磁场矢量

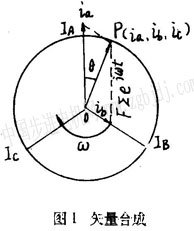
由图1可得如下方程

整理并解方程得

同理可得

当然，这些也可用电磁场的理论求得，结果相同。它们是一组相位差为120o的双峰曲线函数，其波形如图2所示。

从图2可看出，当三相步进电动机工作于单三拍、双三拍、三一六拍等任意一种步进运行方式时，其相电流值仅仅是电流波形上的特殊点，如图2中的pl，p2,p3，p4……。它们在一个周期内分别位于0o，60o，120o，180o，240o圆周角上，其幅值等于一个单位，即步进方式运行时，相电流的额定值。同时还可看出，相电流的每个周期，相当于步进电机步进方式运行时，三一六制的六步，或单三拍的三步。换言之，如bfll0型步进电动机。上述双峰曲线每80个周期，可使它旋转一圈。2 sv系列步进电机同步矢量伺服系统

sv系列步进电机同步矢量伺服系统是实现上述原理的典型线路之一，该系统由函数发生器、功率驱动器、及保护电路等部分组成，系统框图如图3所示。

2.l函数发生器

为了实现直接数字化控制，需将所得出的相电流函数式进行离散。如对上式中进行离散得出

式中n为离散一个函数周期所划分的合成矢量点数，它由实际所需要的分辨率确息；n为随机输入的脉冲数，n与，n均为正整数。实现函数离散表达式的函数发生器由一个n进制可逆计数器。rom及d／a转换器等组成，原理如图4所示。

离散函数值固化于rom中，输入脉冲改变计数器的状态，对rom选址，把从rom中所取出的相应数据，通过d／a转换器使函数值重现于输出端，为下级功率驱动器提供相电流函数双峰曲线信号。

2．2功率驱动器

功率输出级采用先进的pwm技术，输出的双峰曲线电流，直接驱动步进电机绕组。

2．3电源及保护电路

对小型步进电机和对转速范围要求不高的功率步进电机，一般采用固定电压直接供给驱动级；对大、中型功率步进电机和在要求调速范围较宽的使用情况下，则采用变压电源(采用f-v变频变压技术)以提高系统的矩一频特性，并降低输出驱动级的功耗，减少发热现象。

保护电路采用高速自动保护技术，在发生过压，短路或过流时，不致对系统造成致命性损坏。

现以bfl10型步进电动机为例，说明sv系列步进电动机同步矢量伺服系统中ⅳ的选择、进给脉冲、控制精度及分辨率之间的关系。为了兼顾与步进电动机直连的大多数常用传动丝杠(如螺距为2、3、4、6、8、12mm等)，sv系列伺服系统一般取n=90,因此，步进电机定子所具有的等强度合成磁场矢量点数即等于90x 80=7200个，若与步进电机相连接的传动机构为每转位移6mm，则在开环控制时，每12个脉冲位移10μ／m。进给脉冲与控制位移之间以一定数量的脉冲列为当量单位，并非步进方式的“一对一”关系，这对构成闭环控制系统尤为重要。

步进电动机绕组在函数波形为双峰曲线的相电流激励下，前沿平滑上升，克服了绕组电感在常规脉冲驱动线路作用时，使相电流不能突变而产生的过渡过程，有效地抑制了步进电动机运转时的振荡和升速过程中的共振等现象。在高速运转时，相电流呈近似矩形，因此，大大提高了步进电动机的高速矩频特性。步进电动机的转速与输入脉冲频率成正比，当输入脉冲频率为120hz时，步进电动机转速为lr／min；实测空载*高转速超过3000r／min此时，输入脉冲频率按某种设定规律变化时，步进电机转子亦相应作升速、降速、恒速运行。改变可逆计数器的计数方向，即可改变步进电机的旋转方向。也就是说，当直流伺服系统是以o～±10v输入电压控制直流反转从0到*高转速变化时，sv系列步进电动机同步矢量伺服系统则是以输入脉冲频率从0开始变化，来控制步进电动机转速的。系统的阶跃响应，外特性硬度等均可与同功率直流伺服系统相毗美。系统采用ttl—数字电路电平，可与计算机直接接口。

提高步进电动机定子恒模合成磁场矢量等分点的个数，可提高步进电动机的分辨率和控制精度。如在郑州某厂的应用实例，bfll0型三相步进电动机，取n为125，(曾选用n=250)，步进电动机定子一周合成矢量点数即为125×80=10000个，在机床上与5mm滚珠丝杠直连，组脉冲当量为每1／μm两个脉冲，经反复实用测量，开环控制精度±2μm，重复定位精度±1μm，加工表面粗糙度为rao．04μm，达到了加工工艺的高精度要求，当然，控制精度的进一步提高，必须采用闭环系统，其原理框图如图5所示。

如果将步进电动机内部绕组按三相交流电机改接，即成为一个集中绕组的三相交流步进电动机，这时定子中产生的均匀圆周旋转磁场的相电流，即大家熟知的三相正弦交流，其*大幅值可减小为步进电机额定相电流的一半。

3结语

理论上，步进电动机定子可以用建立恒模合成磁场矢量的方法进行“无限”等分，以任意提高步进电动机的分辨率，但由于磁性材料的非线性和步进电动机本身的结构以及工艺技术等各方面的问题，实际上，步进电动机的定子在相电流激励下产生的合成磁场并非**均匀。

在一个函数周期内，任意两个相邻脉冲问形成的定子磁场矢量角差，在相电流函数变化率较大与较小时相比较，与理论上的均匀性存在有偏差，因而影响步进电动机转子微量转角的均匀性(但每个函数的同期偏差基本保持一致)。这些，一方面可以从修正函数入手，另一方面，希望步进电动机生产厂家能在均匀性方面进行改进。

在函数电流驱动下的步进电动机已失去了其原来的“步进”意义，电机本身在该系统中仅作为伺服电机来使用。制造厂家应尽量提高同一体积电机的转矩和磁饱和裕量，以便开发出一种*完善的自适应驱动系统。

1 引言

步进采用微步驱动技术，除了提高电动机的分辨率以外，很重要的目的是为了提高其转动的均匀性。常规的步进电动机系统在低速运行时，有明显的步进感。把一整步分成很多小步，转动的均匀性自然要提高，但是，微步驱动的步进电动机系统其角速度稳定度有何特点，与细分数有什么关系，角速度稳定度能达到什么水平，还受哪些因素的影响和限制等一系列问题，有必要搞清楚。以利于应用系统的设计者正确采用步进电动机的微步驱动技术，同时也是设计制造者所需要了解和掌握的。

为清楚起见，并且能有量的概念，文中给出一个微步驱动系统的实例。

2频域划分及角速度波动的特点

步进电动机的平均转速与控制脉冲频率(fcp)成正比，与逻辑通电状态数(m)及转子齿数(zr)成反比，即

平均转速：

或平均角速度：

式中m——整步方式的逻辑通电状态数，

通常等于相数

n1——整步包含的微步数，即细分数

步进电动机运行时，根据其运动形式的特点，可将整个频域分成若干频段。典型的划分是将整个频域分为极低频、低频和高频。

2．1极低频

即控制脉冲的周期或间隔时间大于停止时间(ts)的频域。电动机每走一步都是单步响应过程，电动机按其自然频率振荡可衰减到静止。按式(2)，电动机的平均角速度很小，但是在自由振荡过程中*大角速度可以达到相当大的值。实际上自由振荡过程中若不计衰减其*大角速度的值为：

可见，在该频域内电动机的角速度波动很大，在其正的*大值和负的*大值之间变化。

2．2低频

在这个频段内，控制脉冲的间隔时间比停止时间小，单步的角速度振荡不能衰减到零。但是控制脉冲的间隔时间比自由振荡周期的要长，所以一般有过冲或超调。在这个频段内起动电动机时，第二步的初始条件比较复杂，在不利的情况下可能产生明显的振荡，包括

fcp=f0(6)

这是通常所说的低频共振点。

2．3高频

在这个频段内，控制脉冲的周期小于自由振荡周期的1／4，所以在这一频段内电动机起动时，第一步的角位移肯定不会超过一个步距角，即产生滞后的动态误差。电动机连续稳态运行时，也就不会有步进感觉。于是把

fcp=f0(8)

作为步进电动机进入高频运行频域的分界线。也就是步进电动机进入比较连续平稳运行域的分界线。由该频率决定的电动机的平均角速度为：

以一台典型的四相混合式步进电动机为

例，它的相数，m=4，转子齿数zr=50，如自然频率f0=100hz，在通常整步方式下运行，代入式(9)得：

就是说，这种典型的步进电动机系统，只有在转速高于120r／min时才进入连续平稳运行区。为了让这台电动机在第100r／min或更低的转速平稳运行，需采用微步驱动技术，细分数愈大，按式(9)进入连续平稳运行的平均速度愈低。若上述电动机取细分数n1=1024，则：

即转速降到8．5min转lr仍属连续平稳运行域。另外，即使在极低频不连续运行域，角速度的波动也随着细分数的增大而显著减小，这时角速度波动的极限值由式(4)表示，它与步距角成正比，或者说与细分数成反比。

3实验研究

实验装置是一套角速度测试系统，其框图如图1所示。

被试电动机是由哈杭电伺服技术研究所研制，用于微步驱动系统，该电机为68byg2102型二相混合式步进电动机。基本技术数据为，转子齿数zr=102，相绕组电阻r=50ω，静态相电流i=0．3a，保持转矩tk≥0．6nm。所配驱动器也是哈杭所研制的二相电动机微步驱动器，细分数可变，nl=1，2，4，……，526，1024。

图2表示一组角速度波形的测试结果，测试时保持电动机的平均角速度不变，为250ms走n1微步，就是说0．25s走一整步或1／4齿距，平均角速度的值为：

图2a为极低频情况下角速度波形的示例。图中可以看出，角速度自由振荡的周期大

约为，t0=5ms，所以其自然频率为：

曲线表明自由振荡的停止时间大约为

ts=40ms。图la对应的是nl=4，fcp=4nl=16．

属于极柢频域。曲线上可以看出角速度*大值达：

=56 rad／s(电角度)=0·549 rad／s约为平均角速度的9倍。

图2b对应于，nl=32，fcp=128脉冲／s，

属于低频频域。角速度不会衰减到静止，但仍有较明显的振荡特征。

图2c和图2d分别对应于，nl=256，fcp=1 024脉冲／s和nl=1 024，fcp=4 096脉冲／s，都属于高频频域。电动机进入连续平稳运行域，角速度波形中没有自由振荡波动的影响。应指出的是，图中曲线显示的小的波动是测试系统不完善造成的，它具有明显的工频干扰的特征。不计这些工频干扰讯号，可看出角速度也有一些波动，在一整步范围内大约变化一个周期，即对于一个齿距的变化周期呈4次谐波的特征。这时角速度波动的**值甚小，在所示的例子中：

≈7．5 rad／s(电角度)一o．073 5rad/s