
阳泉西门子模块供应代理商阳泉西门子模块供应代理商阳泉西门子模块供应代理商阳泉西门子模块供应代理商阳泉西门子模块供应代理商
| 模块 | 6ES7142-3BH00-0XA0 |
| 模块 | 6ES7288-3AE08-0AA0 |
| 模块 | 6ES7288-2DT16-0AA0 |
| 模块 | 6ES7288-3AR04-0AA0 |
| 交换机 | 6GK5005-0BA00-1AB2 |
| 交换机 | 6GK5008-0BA00-1AB2 |
| 触摸屏 | 6AV6643-0CD01-1AX1 |
| 模块 | 6ES7288-5CM01-0AA0 |
| 电源 | 6EP3436-8SB00-0AY0 |
| 触摸屏 | 6AV2123-2MB03-0AX0 |
| 电缆 | 6XV1840-2AH10 |
| 触摸屏 | 6AV2123-2GB03-0AX0 |
| 底座 | 6ES7193-6BP00-0BA0 |
| 底座 | 6ES7193-6BP00-0DA0 |
| 模块 | 6ES7288-3AQ02-0AA0 |
| 模块 | 6ES7141-3BH00-0XA0 |
| 模块 | 6ES7193-6PA00-0AA0 |
| 模块 | 6ES7288-3AE04-0AA0 |
| 模块 | 6ES7288-2DE08-0AA0 |
| 模块 | CTS7114-1BD20-0620 |
| 模块 | 6ES7288-3AM03-0AA0 |
| DP电缆 | 6XV1830-0EH10 |
| 内存卡 | 6ES7954-8LE03-0AA0 |
| 模块 | 6ES7288-3AM06-0AA0 |
| 模块 | 6ES7241-1CH32-0XB0 |
2)电感元件的交流电路
在上一次学习电路基本定律的相量形式的时候,我就有提到过,在正弦交流电路中,流过电阻元件的电流与电阻元件两端的电压同相;流过电感元件的电流滞后于电感元件两端的电压90°;流过电容元件的电流超前于电容元件两端的电压90°。下图32-6(a)所示为一电感元件的交流电路。
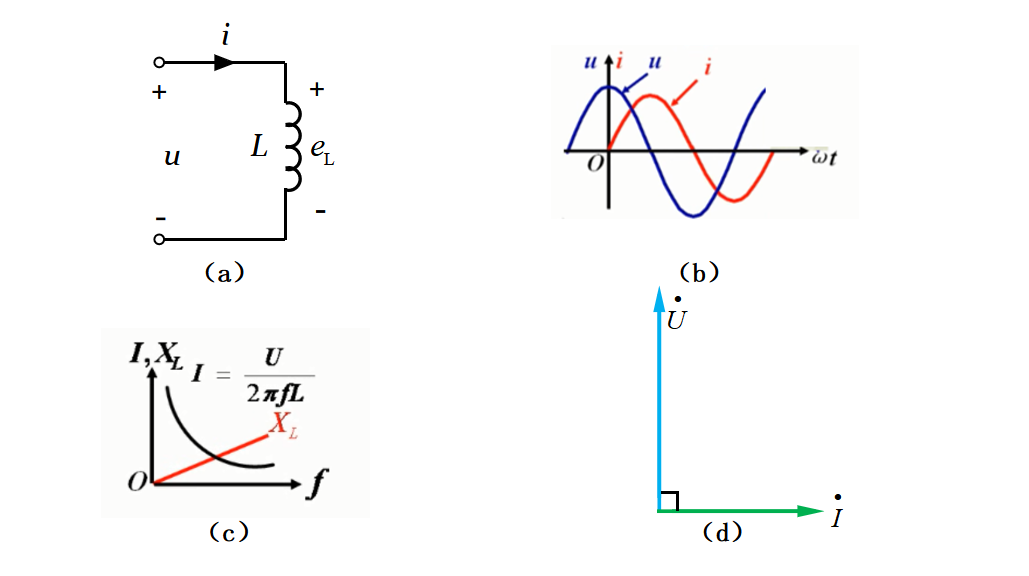
图32-6

图32-7
电感元件的交流电路中电压与电流的关系如图32-7(1)所示。根据上文电感元件的电压电流公式,设流过线圈的电流i是初相角为零的正弦量,代入(1)式,得到的结果如图32-7(2)式所示,微分公式的变换过程大家了解一下就行,我们要知道的是结果。
比较图32-6(b)中的电压与电流的波形图和图32-7(2)式中的电压与电流的瞬时值表达式,可以发现,电压和电流的频率相同,此时电压的相位是超前电流相位90°的。从图32-7的(2)式可得,电压U的有效值是等于IωL的。
类似于欧姆定律U =IR,在电感元件的交流电路中,如图32-7的(3)所示,定义感抗XL=ωL,可得U =IXL。在交流电路中,阻抗包含了电阻和电抗,而电抗又包含感抗和容抗,这里的感抗就是XL。
由角频率ω与频率f的关系ω=2πf,如图32-7的(3)所示,可得感抗XL=2πfL,即感抗XL是频率f的函数,如图32-6(c)所示,感抗XL与频率f的函数曲线为过原点的直线,而电流I与频率f的关系为反比例函数。
正如图32-7(4)所示,当在直流电路时,频率f为零,此时线圈感抗XL为零,在交流电路中,随着频率f的增大,感抗XL也增大,即电感具有通直阻交的作用,或者可以这样说,电感元件具有通低频阻高频的特性。
根据图32-7(2)式,电压超前电流90°,可画出电压与电流的向量图,如图32-6(d)所示,即电压相量与电流相量夹角为90°。
电压与电流的相量式如图32-7(5)所示,结合之前在学“正弦量的相量表示”时所学的复数知识(复数F =a jb),其中的j为90°旋转因子,可以得到电压相量除以电流相量的商为jωL,这其实就是电感电路复数形式的欧姆定律。
在上文中,我们知道了电感元件是储能元件,在交流电路中,它把吸收的电能转化为磁场能量存储在磁场中。同是图32-6(a)所示的电感元件的交流电路,电感元件的功率关系如图32-8所示。

图32-8
根据上文提到的瞬时功率和平均功率的定义,电感元件的瞬时功率p的表达式为图32-8(1)式所示,其中三角函数的变换大家看看就行,不懂也没关系,记住就可以了。
根据瞬时功率p的表达式画出其波形右图(a)所示。结合电压u、电流i和瞬时功率p的波形图,可以发现,当电压与电流的方向一致时,电感元件向电源吸收能量并存储;当电压与电流方向时,电感元件向电源释放能量,这个吸收和释放能量的过程是可逆的,且吸收的能量和释放的能量相等。
也就是说,电感元件在存放能量的过程中是没有消耗能量的,只是和电源进行能量的交换。由此可推理出电感元件的平均功率为零,正如图32-8(2)式所示。
在这里先引入一个新的概念:无功功率Q。无功功率是指在具有电抗的交流电路中,能量在电源和电抗元件(电容、电感)之间不停地交换,交换率的大值称为“无功功率”。也就是说,无功功率是用于衡量电感或电容电路中能量交换的规模,用瞬时功率达到的大值表征,如图32-8(3)式所示,取瞬时功率p的大值UI,用字母Q表示,单位是乏(var)。
所谓无功,并不是说它是无用的,这是相对于有功功率而言。无功功率的更多内容在此就不展开讲述,大家感兴趣的可以拓展自学。
(3)电容元件的交流电路
在学习了电感元件的交流电路的基础上,学习电容元件的交流电路就会简单很多,因为它们两者有很多相似的地方。如图32-9(a)所示为一电容元件的交流电路。
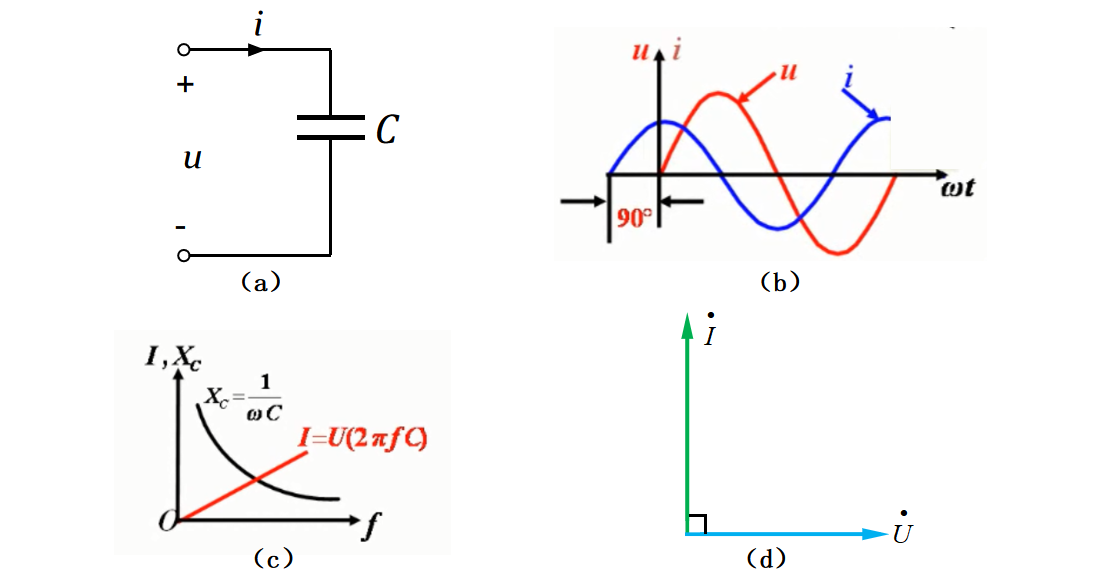
图32-9
结合上文提到的电容元件的电压与电流的基本关系式,如下图32-10(1)所示,设电压u初相角为0,其瞬时值表达式如图32-10(2)式所示,将电压u的瞬时值表达式代入(1)式中可以得到此时电流i的瞬时值表达式,微分公式的变换过程大家不用在意,记得结果就行。
根据图32-10(2)式中电压与电流的表达式,可以发现,在电容元件的正弦交流电路中,电流是超前电压90°(电压滞后电流90°)的,且它们两者的频率相同,其波形图如图32-9(b)所示。从图32-10(2)式中也可以看到,电流的有效值I是等于UωC的。

图32-10
根据电压与电流的关系I =UωC,同样是类似于欧姆定律U =IR,如图32-10(3)所示,定义容抗XC=1/ωC,则U =IXC。
关于容抗,上文也说了,它和感抗统称为电抗。同样的,由角频率ω与频率f的关系ω=2πf,如图32-10的(3)所示,可得容抗XC=1/2πfC,即容抗XC也是频率f的函数,如图32-9(c)所示,容抗XC与频率f的函数曲线为反比例函数曲线,而电流I与频率f的关系曲线为过原点的直线,和电感元件的感抗与频率关系曲线相比较,大家是否发现了它们之间的差异?
正如图32-10(4)所示,当在直流电路时,因为频率f在分母中,频率趋于零时,此时容抗XC趋于无穷大,相当于开路;在交流电路中,随着频率f的增大,容抗XC减小,说电容器有隔直作用。
和电感元件的电压相量、电流相量类似,电容元件的电压相量与电流相量关系如图32-10(5)所示,画出它们的向量图如图32-9(d)所示,电压相量与电流相量的夹角为90°。结合之前所学的复数知识,当90°旋转因子为-j时,对于相量顺时针旋转90°,由于电压滞后电流90°,此时图32-10(5)中的电流相量乘以-j而不是j。
和电感元件一样,电容元件也是储能元件,在交流电路中,它把吸收的电能转化为电场能量存储在电场中。同是图32-9(a)所示的电容元件的交流电路,电容元件的功率关系如图32-11所示。
由图32-11(1)所示,电容元件的瞬时功率和电感元件的瞬时功率相似,根据其瞬时功率p的表达式画出其波形右图(a)所示。
结合电压u、电流i和瞬时功率p的波形图,可以发现,当电压与电流的方向一致时,电容元件向电源吸收能量并存储;
当电压与电流方向时,电容元件向电源释放能量,这个吸收和释放能量的过程是可逆的,且吸收的能量和释放的能量相等。
也就是说,电容元件在存放能量的过程中是没有消耗能量的,只是和电源进行能量的交换。由此可推理出电容元件的平均功率为零,正如图32-11(2)式所示。

图32-11
为了同电感电路的无功功率相比较,和上文的电感元件一样设电流的初相角为零,此时电压与电流的瞬时值表达式如图32-11(3)所示,则电容元件的瞬时功率p的大值为-UI,而无功功率QC为图32-11(4)所示。
单一参数正弦交流电路:电阻元件的交流电路、电感元件的交流电路与电容元件的交流电路的内容比较多,大家把三者结合起来,相互比较就可以发现,它们的相似之处有很多,记住其中一种电路的相关特性,就可以联想起其余电路的相关特性。
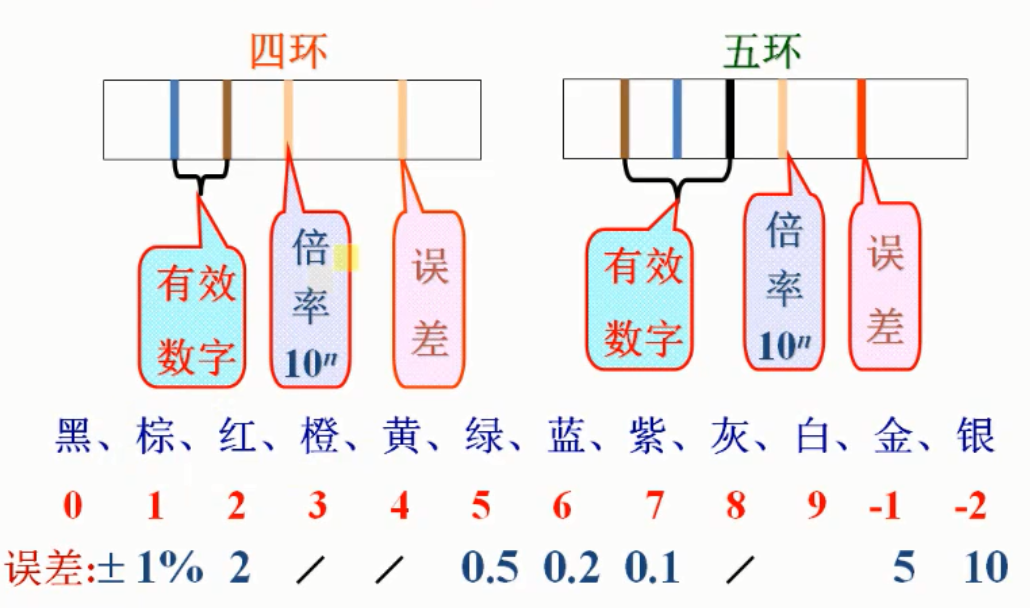
图32-12
在电子技术及电力电子技术中,要经常用到具有电阻值的元件“电阻器”和具有一定电容值的元件“电容器”,电阻器也叫定值电阻,简称电阻,而电容器也叫定值电容,简称电容。
一般电阻器和电容器都是按标准化系列生产的,它们有着同一的标称值、允许误差等。
例如电阻器可以通过查看其色环而知道它的一些参数,如上图32-12所示就是电阻器的色环表示法。
阳泉西门子模块供应代理商 阳泉西门子模块供应代理商