6ES7214-1HG40-0XB0西门子CPU1214C
步进及其驱动器在刺绣机上获得了广泛的运用。电脑刺绣机是80年代国外纺织机械中的*新产品。它运用微机技术,实现刺绣整个过程的自动化,大大提高了刺绣产品的质量和生产效率。
电脑刺绣机是的产品,主要由刺绣机身、系统、计算机系统、驱动执行机构系统、刺绣框、刺绣头以及信号等部分组成,其刺绣动作过程为,由磁盘或纸带机将花样信号送入计算机,经计算机处理后送入步进电机驱动系统和主轴控制系统,*后由动力系统带动刺绣框、刺绣头协调运动,刺绣开始。
在刺绣过程中,步进电机驱动绣框运行是*重要的环节,它直接影响到绣品的质量、刺绣效率和噪声大小。
电脑刺绣机是使用微机对步进电机的速度进行控制,控制的实质就是控制电机驱动负载时的运行曲线,首要的是进给脉冲时刻的计算,是一种软件控制方法。通常的设计方法是使步进电机按加速、匀速、减速的曲线运行,离线计算出定时时间,把它们写入内存中,实现步进电机速度控制软件化。这种方法的缺点是计算机只能按照事先给定的速度曲线对步进电机进行控制,无法按照刺绣工况的变化随时修改速度曲线的参数,使步进电机在合理的状态下运行。本文介绍一种适合在电脑刺绣机上使用的步进电机的运行曲线及其计算方法,实现了定时参数的在线计算。
2实现的曲线及其参数的计算
2.1实现的曲线(见附图)
考察如下的正弦函数:

式中π=3.1415926,t为步进电机的运行时间。实现这种函数曲线的优点为:
a.由于曲线平滑,步进电机驱动负载运行平稳、柔和、噪声小。
b.满足步进电机慢起动、慢停止的特性。
c.有明确的数学表达式,易于在线计算和实现。
d.对于不同的刺绣工况,可通过改变参数a和t实现。
2.2计算
假设步进电机驱动负载时的某工况为,在t时间内需要步进电机运行n步,电机的*高运行频率为fm,起始频率和终了频率都为零。运行曲线为式(1)的f(t),把t分为n份,即△t1,△t2,……,△tn,t=△t1+△t2+……+△tn。令:
t1=△t1
t2=△t1+△t2
tn=t=△t1+△t2+……+△tn
如附图所示,令f(t)在t轴上半部所围成的面积为n,f(t)与△t1, △t2,……△tn所围成的面积都为1,即:
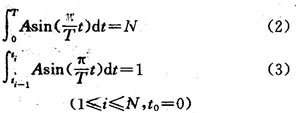
参数a的确定
a为步进电机的实际*高运行频率,按式(2)可求出a的值。

必须保证a应小于给定的电机*高运行频率,否则会引起严重后果。
2.2.2 参数t(i=1,2,……,n)的确定
按式(3)可得:

由于t0=0,按式(5)可递推出t1,t2,……,tn-1的值。
△ t1=t1
△ t2=t2-t1
.
.
.
△ tn=t-tn-1
2.2.3进给脉频率fi(i=1,2,……,n)的计算
fi=1/△ti(i=1,2,……,n) (6)
不难证明,fi为函数f(t)=asin(π/t ·t) (ti-1≤t≤ti)上的一点。
3应用举例
在某电脑刺绣机产品上,步进电机驱动
绣框水平前后左右移动,脉冲当量为0 .lmm,刺绣某针迹长度为4ram(相应的脉冲数量为n=40),给定的时间为30ms,步进电机的起蛄和终了频率都为零,计算各进给脉冲的时间和相应的运行频率。
4
实现曲线是步进电机平均建度的连线,在某一进给脉冲间隔内,它又是理想的正弦曲线某一时刻的速度,实现的精度是曲边梯形和单位矩形面积之差的**值。这种方法实班的关键在于所使用的计算机要有三角函数的处理能力,且有较高的运算速度,否则难以胜任高速刺绣。
步进的设计和优化设计中*重要的是性能指标的预测,由于步进电动机的结构和运行条件特殊,人们在计算过程中往往要作某些假设,例如忽略磁路的饱和或是假定铁心部分的磁压降与转子位置无关等,以求得到简化,这自然会给计算结果带来一定的误差。为了充分考虑电机磁路的饱和对其性能的影响,本文将以样机bf36型磁阻式步进电动机为例,采用有限元数值解法,并借助网格自动剖分技术,对整个电机的求解区域进行磁场分析,求得电机磁场的磁共能,进而计算出电机的静态转矩。磁阻式步进电动机的定、转子齿形尺寸的不同,将影响电机磁路的磁导和电机磁场,从而影响电机的性能。
2静态转矩特性的有限元数值计算
bf36型三相磁阻式步进电动机的结构如图1所示,定子上共有6个磁极,每极上有3个矩形齿,辖子上有zr=20个均匀分布的矩形齿,定转子齿矩卢18度。电机的un= 24v,ln= 0.15a,可以单相通电,也可以双相通电运行。

用有、限元数值解法计算磁阻式步进电动机的静转矩。可直接利用电机磁场的磁共能计算电磁转矩的公式[1]。

式中θr一转子的角位移,radθ一转子的角位移,
为了算出电机的静态转矩特性,即矩角特性,就必须研究电机定子磁极线圈在不同电流下,以及转子相对定子有不同位置时的磁场分布情况。由于在齿距t范围内,在 的位置电机磁场对称,故只需研究半个齿距,即9度范围内各个位置的磁场情况即可。
的位置电机磁场对称,故只需研究半个齿距,即9度范围内各个位置的磁场情况即可。
设定转子齿中心线对齐时θ=0,根据电机的结构、+通电方式和磁场对称性,可选定半个电机的空间作为电机磁场的求解区域,图2示出这时求解区的网格剖分。

在某一θ值下磁极线圈通入电流后,经二维磁场的有限元计算[2]可得出此时求解区域内部节点的矢量磁位a值、各单元的磁通密度以及绘出求解区的磁力线分布。图3展示了θ=1度时,a、b两相通电的磁力线分布,再经后处理的计算,便可求得通电的磁极线圈所匝链的总磁链ψ。改变电流的数值,再计算该θ位置的磁场和磁极线圈匝链的总磁链新值。这样,重复多次计算后便可得到一组不同的电流及其所产生的磁极线圈磁链,即得出在此转子位置θ下电机的电流与线圈磁链之间的关系ψ=f(i).

如果转子在空间从θ=0起按顺时针方向每转过1度,再重复上述计算,直至θ=9度止(这在有限元数值分析中借助网格自动剖分技术后是容易实现的),从而得出电机在所有10个定、转子相对位置的磁链与电流间的关系。图4是a相绕组通电状态下θ=0和θ=1度时电机的ψ=f(i)关系曲线。从而可用simpson积分法‘3’分别求出在某一电流下各个θ位置的磁共能遍wm,例如i= in=0.15a,θ=0时的磁共能值就是曲边形oaco的面积,θ=1度时的磁共能则为曲边形obco的面积。重复上述步骤,便可求出在此电流下θ=0.1度.2度……9度时所对应的10个电规的磁共能,即有wm对应于0的10组对应值。再用三次样条插值函数的微分公式(4)就能求得磁共能wm。对θ导数,并根据式(i)即可得出步进电动机的静转矩特性曲线t=f(θ)。图5和图6表示该电机在额定电流下单相通电和两相通电时计算所得的静转矩特性。图7和图8则分别表示所对应的实测结果。两者相比较,*大静转矩的误差在单相通电时是百分之5 .41,两相通电时为百分之7.34。

3齿形尺寸对*大静转矩的影响
进电动机不同的定转子齿形配合作过一些基础研究,以探明它们对电机性能的影响,所得出的是,定转子的齿形应选用矩形为好。在齿形尺寸上,例如齿高、齿距和齿宽彼此之间是否存在一个**的配合,为此,我们对该样机采用不同的齿高与齿距的比值(在同一槽宽时)以及不同的齿宽与齿距的比值(在同一槽高时),进行*大静转矩的计算,表l和表2分别列出它们的计算结果(均为两相通电状况),其中表示样机的实际尺寸。由表可见,磁阻式步进电动机定转子齿形除了采用矩形之外,其齿高应尽量接近齿距,齿宽则约为齿距百分之的37.5。

4
a.为充分考虑电机的饱和因素,本文从整个电机磁场的磁共能出发,计算了反应式步进电动机单相通电和两相通电的静态转矩特性,且计算值与实测值基本接近,说明此理论计算方法是正确的。
b.当齿高/齿距≈_l和齿宽/齿距≈0.375时,磁阻式步进电动机可获得较大的静态转距,这在工厂的生产中可作参考。